What are Rule Attributes?
Some Attributes Basics
    Mutually-Recursive Rules
    The Role of Empty Strings
How are Attributes Determined?
    Rule Types
    The Opcode Rules for Attributes

What are Rule Attributes?

Attributes are aspects of the rules of a grammar that exist beyond the syntax and semantics of the grammar. It is entirely possible to write a well-formed ABNF grammar that is unparsable due to problems with its recursiveness. Identifying and computing these attributes is one of the most complex aspects of generating a working parser from an ABNF or SABNF grammar. Therefore, I'll try to describe attributes and their computation some in detail here.

It is well known that left-recursive rules are unparsable. Consider

S = S "a" / "b"

The first step in matching any input string is to expand the rule S. It is also the second and all future steps. In other words, the parser will simply recurs the rule S until there is a stack overflow exception. Left-recursion is therefore an attribute (or aspect or quality or characteristic) of the rule S that is important to know. APG regards left recursion as a fatal attribute of the rule S and scans each input SABNF grammar to determine in advance whether any rule is left-recrusive.

But there is more. APG actually identifies six different attributes and evaluates them for each rule in the grammar, three of which are fatal. These are the six attribute definitions with a simple example of each.

top

Left Recursion**

S = S "a" / "b"

Left recursion is a fatal attribute as discussed above.

Right Recursion**

S = "a" S / "b"

Right recursion is a non-fatal attribute and generates repetitions. The above rule matches strings of the form aⁿb, n> 0.

Nested Recursion**

S = "a" (S/"ab") "b"

Nested recursion is a non-fatal attribute and differentiates between regular and context-free expressions. Rules that do not exhibit nested recursion are equivalent to regular expressions. The above rule matches strings of the form aⁿbⁿ, n > 0, a well-known example of a rule that can't be represented with a regular expression.

Cyclic Recursion**

S = S

Cyclic recursion is a fatal attribute. It has no terminal nodes and cannot represent any string.

empty**

S = *"a"
E = ""

The empty attribute is non-fatal but, as we will see later, extremely important in the determination of the recursive attributes. The rule S can be, but is not necessarily empty. It matches the strings aⁿ, n >= 0. On the other hand, the rule E only matches the empty string.

finite**

S = "a" S

The finite attribute is fatal if it is false. The above rule only matches infinite strings. A rule must have at least one branch or alternative that ends with a terminal node to be finite.

top

Some Attributes Basics

Attributes are determined by walking the syntax tree of opcodes. The procedure is to walk down to a terminal node, set the known attributes of the terminal node and then apply fixed modification rules at each of the non-terminal nodes walking back up the tree. But what about recursive rules? They have infinitely deep syntax trees. The saving grace is that all the attribute information can be had from a single expansion of each rule. That is, APG will walk a Single-Expansion Syntax Tree (SEST) of the rule's opcodes to determine the attributes. Let's look at an example.

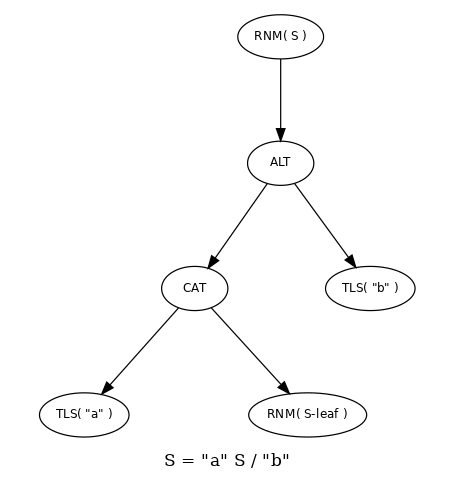
Here, the right-recursive rule S is expanded only once. When it is encountered a second time it is considered a special type of terminal node, called here, somewhat arbitrarily, a leaf node. Let's walk this SEST and see how it is done. In this simplified example a lot of details and special cases will be overlooked, but it will reveal the essentials of the algorithm.

The TLS terminals are non-recursive, finite and possibly empty, but non-empty in this case. But how do we handle the S leaf terminal node? The answer is to ask, "what would the attributes be if the rule were cyclic with no non-terminals in the tree?" For

S = S

We would say the attributes were left, right and cyclic. So that is what we use for the S leaf node. In a correctly written grammar, the non-terminal nodes in the tree between the root S node and the S leaf node will modify those fatal attributes to non-fatal ones. Let's see how that works out. Moving up to the CAT node, its basic rules are:

if any child is not empty, CAT is not empty
if any child is not finite, CAT is not finite
if the right-most child is right-recursive, CAT is right-recursive
if the left-most child is left-recursive, CAT is left-recursive
if all children are cyclic, CAT is cyclic In this case, we see that CAT is non-empty, finite, and right-recursive.

Moving up to the ATL node, its basic rule is:

if any child attribute is true, the corresponding ALT attribute is true

In this manner, we see that ALT and hence S is not empty, finite and right-recursive.

That's the basic idea. Walk the SEST of opcodes, work backwards from the known attributes of the terminal nodes and use combination rules at the non-terminal nodes to migrate the final attributes to the root rule.

top

Mutually-Recursive Rules

Consider the grammar

S = "s" A B
A = "a" B / "y"
B = "b" A / "x"

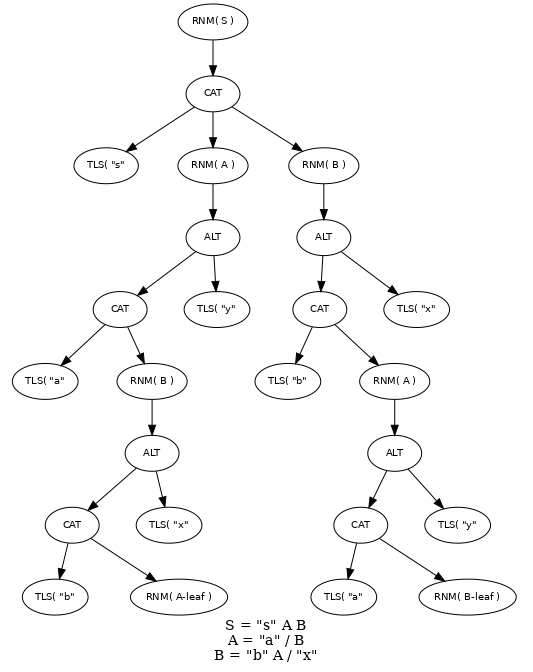
Notice that A and B are recursive and refer to one another. That is, they are "mutually recursive". At first glance that would appear to be a problem in that we would need to know the attributes of A to determine those of B and vice versa – a catch-22.

However, the way out of this is to first make the observation that S is non-recursive. But if we include the recursive attributes of A and B, right-recursive, then we would incorrectly compute S to likewise be right-recursive. So we see that to compute the recursive attributes of S we need to ignore the recursive attributes of A and B (but not the empty and finite attributes.)

So this is our way out of the catch-22. When computing the recursive attributes of A we ignore those of B. In fact, the general algorithm is to ignore all recursive attributes of all rules accept the rule under consideration (the root of the SEST.)

top

The Role of Empty Strings

The empty attribute can be true or false. Both are acceptable. Neither is fatal causing the parser to fail. However, the empty attribute plays a vital role in determining the recursive attributes. Consider the following rule.

S = *"a" S / "y"

It looks a lot like the right-recurive example above. But there is a big difference. Because the repetions operator * can accept an empty string, this rule is actually left recursive. This means that our CAT rules have to be modified to read

if the left-most non-empty term is left-recursive, CAT is left-recursive.
if the right-most non-empty term is right-recursive, CAT is right-recursive.

top

How are Attributes Determined?

As explained above, the SEST of opcodes is walked for each rule. The terminal opcode nodes have known attributes and the non-terminal opcode nodes have rules for determining their attribute from their children below. The specifics of the actual alogrithms are explained here in more detail. For complete details see the code in rule-dependencies.c and rule-attributes.c.

top

Rule Types

Although they are not used in the determination of the rule attributes, rules are classified into three types for information and display purposes.

N: non-recursive – the rule never refers to itself.
R: recursive – the rule refers to itself, ether directly or indirectly.
MR: mutually-recursive – a group of rules that refer to themselves and every other rule in the group.

The API offers tools to display the rules, by index (the order they appear in the grammar), by name alphabetically, and by type, names alphabetical within a given type or mutually-recursive group. See vApiRulesToAscii and vApiRulesToHtml.

top

The Opcode Rules for Attributes

The terminals have known attributes and can be set directly. All of their recursive attributes are false. All of their finite attributes are true. The empty attribute depends on the terminal operator.

Terminal Operators
terminal operator	attributes
TLS: terminal literal string	empty: true if string length = 0, false if not
TBS: terminal binary string	empty: false (binary string can never be empty)
TRG: terminal range	empty: false
BKR: back reference	empty: inherits from the back-referenced rule
UDT: user-defined terminal	empty: true if e_name, false if u_name
ABG: begin of string anchor	empty: true
AEN: end of string anchor	empty: true

Then there is a group of non-terminal operators that inherit all attributes from their single child except the empty attribute.

Non-terminal operators with single child.
operator	attributes
REP: repetition, n*m	empty: true if n = 0, inherited otherwise
NOT: positive look ahead (&)	empty: true
AND: negative look ahead (!)	empty: true
BKA: positive look behind (&&)	empty: true
BKN: negative look behind (!!)	empty: true

The remaining non-terminal rules get complicated. Here you are mostly referred to the actual code to see how it works.

Complex non-terminal operators.
operator	attributes
ALT: alternation	see `vAltAttrs()` in rule-attributes.c
CAT: concatenation	see `vCatAttrs()` in rule-attributes.c
RNM(root): rule operator	inherit all attributes from single child
RNM(root leaf^†):	left: true nested: false right: true cyclic: true empty: false finite: false
RNM(non-root leaf^‡):	left: false nested: false right: false cyclic: false empty: false finite: false

^† Root leaf is defined as the second occurrence of the root (start) rule on any branch.
^‡ Non-root leaf is defined as the second occurrence of any rule other than the root rule on any branch.

top